## 问题描述
环境：Manjaro
在开机加载时出现上述错误。
解决方法
执行：
sudo pkgfile -u
重启即可。
参考链接：https://forum.manjaro.org/t/failed-failed-to-start-pkgfile-database-update/31731/
本文用于分享和备忘，使用于最新的 Manjaro 版本
过程
本教程仅限使用于 Manjaro 的最新版本 ，Arch 系其他系统使用出错本人概不负责
首先，确认自己具有如下的先决条件：
- 自己的 Manjaro 已经配备好了 archlinuxcn 源，如没有，请按照如下命令添加清华大学的 archlinuxcn 源：
sudo vim /etc/pacman.conf 或 sudo nano /etc/pacman.conf
并在文件中插入以下内容：
[archlinuxcn]
Server = https://mirrors.tuna.tsinghua.edu.cn/archlinuxcn/$arch
勘误：随后应该执行如下命令再继续操作：
sudo pacman -Sy archlinuxcn-keyring
P.S.：上方清华源可以替换为其他源，例如中科大源
- 自己的 Manjaro 已经安装好了 yay，如没有，请按照如下命令安装：
sudo pacman -Sy yay
然后，请按照如下命令进行配置：
sudo pacman -Sy fcitx
sudo pacman -Sy fcitx-configtool
sudo pacman -S base-devel
yay fcitx-sogoupinyin
yay fcitx-qt4
# 以上四步是fcitx和搜狗拼音的配置
执行完后请继续执行如下一条命令：
vim ~/.xprofile
这时你会获得一个文件，在这个文件中加入如下内容：
export GTK_IM_MODULE=fcitx
export QT_IM_MODULE=fcitx
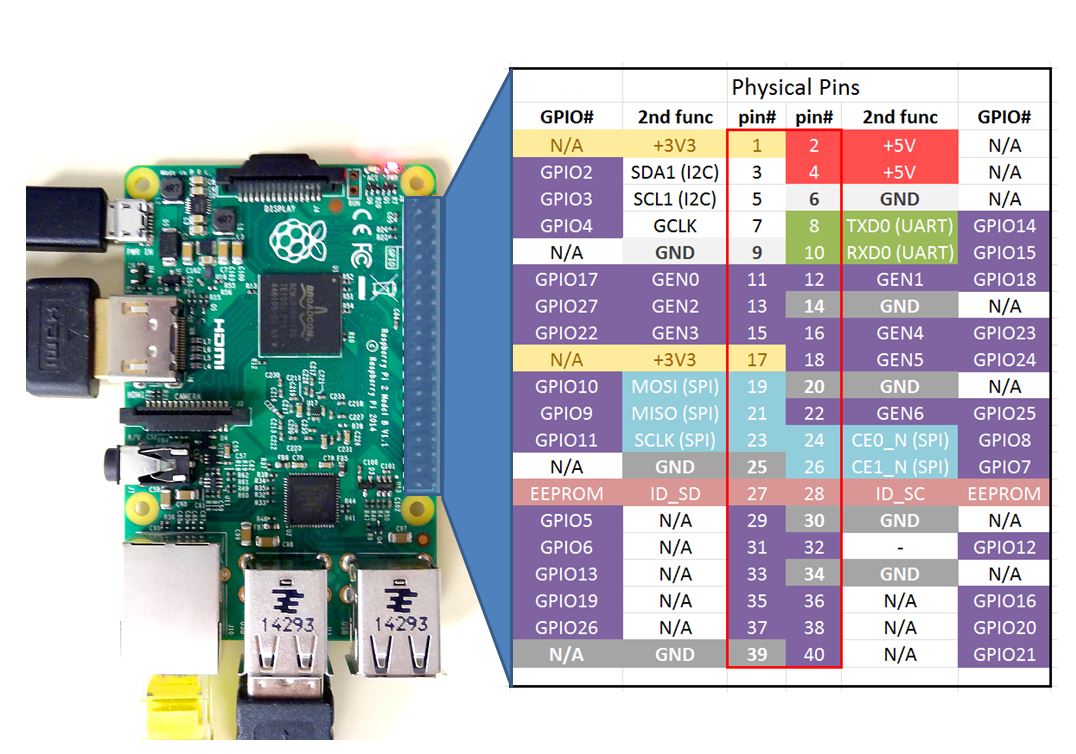
一直以来我都将一块树莓派作为我的服务器来使用，但是夏天到了，散热成了新的难题。既不想让风扇一直转(吵人)，又想让 CPU 温度到达一定程度的时候启动，这确实有些棘手。查阅了相关达人的经验之后，我决定用继电器来解决这个问题。
思路
由于树莓派的控制脚针 GPIO 的电流并不足以带动风扇，所以使用继电器来间接控制风扇。pin2、pin4 直接连接到电源，不受 CPU 控制，这里的电流足够，而继电器的控制端接 pin12，以此来达到间接控制风扇的目的。
经历
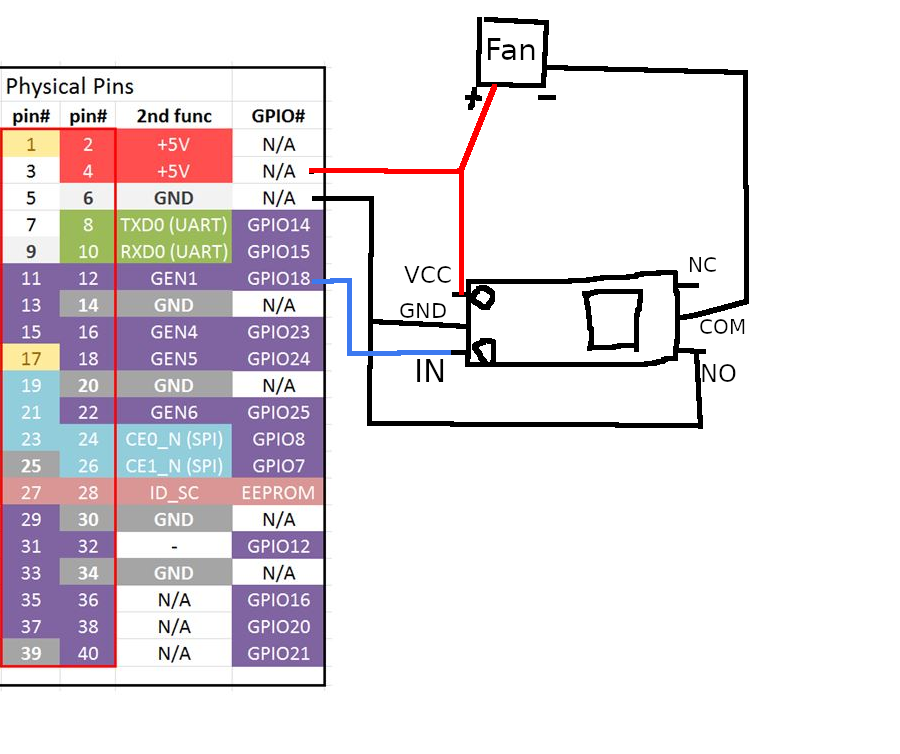
电路
说干就干，在淘宝上不到四块钱买了一个继电器，非常便宜，这里注意要买 5V 电压的。
然后把电路接上，就像这样。此时的控制电路IN接的是Pin12也就是BCM控制方式的18端口。
程序
获取树莓派 CPU 温度非常简单，最终用 Python 编写。首先需要安装 GPIO 控制包。
sudo apt install rpi.gpio
import RPi.GPIO as GPIO
import time
GPIO.setmode(GPIO.BCM)
GPIO.setwarnings(False)
def cpu_temp():
with open("/sys/class/thermal/thermal_zone0/temp", 'r') as f:
return float(f.read())/1000
GPIO.setup(18,GPIO.IN)
is_close = True
while True:
temp = cpu_temp()
if is_close:
if temp > 50.0:
print(f"temp={temp}, open the fan")
GPIO.setup(18,GPIO.OUT)
is_close = False
# 如果已经在开启着
else:
if temp < 45.0:
print(f'temp={temp}, close the fan')
GPIO.setup(18, GPIO.IN)
is_close = True
time.sleep(2)
print(f"temp={temp},is_close={is_close}")
最后使用Screen在后台运行即可。
介绍
二叉树是树的一种特殊情况，规定一个根节点只能有两个孩子节点。如果再规定，左子数中的所有元素都要小于父亲节点的元素，右子树中所有的元素都要大于父亲节点的元素，这样的二叉树就是二叉查找树。找到一个元素的时间复杂度就是 O(logN)。
二叉树的定义是一个递归定义。
定义
我们定义它的数据结构。
/*
二叉查找树的ADT实现
*/
#include<stdio.h>
#include<stdlib.h>
#define ElementType int
typedef struct TreeNode *Position;
typedef Position SearchTree;
SearchTree MakeEmpty( SearchTree T );
Position Find( ElementType X, SearchTree T );
Position FindMin( SearchTree T );
Position FindMax( SearchTree T );
SearchTree Insert( ElementType X, SearchTree T );
SearchTree Delete( ElementType X, SearchTree T );
ElementType Ertrieve( Position P );
struct TreeNode {
ElementType Element;
SearchTree Left;
SearchTree Right;
};
值得注意的是删除(Delete)函数的实现。
介绍
栈是一种特殊的表，规定它只能从栈顶插入数据(Push)，也仅仅只能从栈顶取出数据(Pop)，也就是先进后出(FILO)。它在程序设计中非常重要，例如函数的调用使用的就是栈结构。
栈也同样有两种实现，一种是数组实现，另一种是链表实现。
一般来说，大部分情况下使用数组实现。我们只将很少的数据放入栈中。
数组实现
数组实现的好处是时间复杂度底，仅仅操作一个数组，但是我们在最开始定义栈的时候，必须指定一个固定大小，这导致它失去的灵活性。为了防止栈溢出，我们总是定义一个稍微大一点的数组，但是它也造成的空间的浪费。
定义
/*
栈的数组实现
相比于链表实现，数组实现更为常用。
虽然它有缺点，就是数组的大小是固定的，也就意味着栈的大小是固定的，
所以每次创建栈的时候都要预留一些空间，这样会造成空间的浪费，但是相比于时间开销，这还是划算的。
*/
#define ElementType int
#include <stdio.h>
#include<stdlib.h>
typedef struct StackRecord *PtrToStack;
typedef PtrToStack Stack;
// 栈为空时，栈顶元素的数组下标，这里定义为-1
#define EmptyTOS (-1)
// 规定最小的栈的大小
#define MinStack (5)
int IsEmpty(Stack s);
int IsFull(Stack);
Stack CreateStack(int MaxElements);
void MakeEmpty(Stack);
void DisposeStack(Stack);
ElementType Top(Stack);
void Push(ElementType, Stack);
int Pop(Stack);
struct StackRecord {
// 栈顶的数组下标，栈为空是，它为-1
int TopOfStack;
// 栈的大小，也就是数组的大小
int Capacity;
ElementType *Array;
};
函数实现
int
IsEmpty(Stack s) {
return s->TopOfStack == EmptyTOS;
}
int
IsFull(Stack s) {
return s->TopOfStack == (s->Capacity-1);
}
Stack
CreateStack(int max) {
if (max < MinStack) {
fprintf(stderr, "Stack size is too small.");
exit(1);
}
Stack stack = malloc(sizeof(struct StackRecord));
stack->Array = malloc(sizeof(ElementType) * max);
stack->Capacity = max;
MakeEmpty(stack);
}
void
MakeEmpty(Stack s) {
s->TopOfStack = EmptyTOS;
}
ElementType
Top(Stack s) {
if(!IsEmpty(s))
return s->Array[s->TopOfStack];
else {
fprintf(stderr, "Stack is Empty!");
}
return 0;
}
void
Push(ElementType X, Stack s) {
if(!IsFull(s)) {
s->Array[++s->TopOfStack] = X;
}
else {
fprintf(stderr, "Stack is Full!");
}
}
// 成功则返回1，否则返回0
int
Pop(Stack s) {
if (!IsEmpty(s)) {
s->TopOfStack--;
return 1;
} else {
fprintf(stderr, "Stack is empty!");
return 0;
}
}
void
DisposeStack(Stack s) {
if ( s != NULL ) {
free(s->Array);
free(s);
}
}
链表实现
栈的链表实现与表的链表实现在很大程度上是相同的，它只不过规定了插入和取出的位置只能是栈顶。
介绍
栈可以做一些有意思的应用，例如括号的匹配。在编写 C 程序中，编译器可以检测括号是否匹配，以及哪里匹配错误。这可以轻松的使用栈来实现。
实现
当读取到左括号的时候入栈(Push)，当读取到右括号的时候，将弹出栈顶元素进行比较，检测是否是匹配的符号。如果全部匹配并且栈为空，则括号匹配，否则不匹配。
代码
代码使用数组栈，定义最大栈容量为 20。
/*
字符匹配程序，利用数组栈实现。
匹配 ( [ { 这三种字符
*/
// 引入栈的头文件
#include "squenceStack.h"
#include<string.h>
// 定义最大栈长度
#define MAX 20
int main(void) {
// 创建一个栈
Stack stack;
stack = CreateStack(MAX);
char input[20];
printf("请输入一串字符，以回车结束：");
scanf("%s", input);
printf("你输入了 %s，长度为len=%d\n", input, strlen(input));
int i = 0;
for (i = 0; input[i] != '\0'; i++)
{
int iswrong = 0;
//如果是左括号，则入栈
if (input[i] == '(' || input[i] == '[' || input[i] == '{') {
Push(input[i], stack);
} else {
switch (input[i])
{
case ')':
// 如果匹配，并且出栈成功(未到栈底)
if (Top(stack) == '(' && Pop(stack) == 1)
;
// 否则出错
else
iswrong = 1;
break;
case ']':
if (Top(stack) == '[' && Pop(stack) == 1)
;
else
iswrong = 1;
break;
case '}' :
if (Top(stack) == '{' && Pop(stack) == 1)
;
else
iswrong = 1;
break;
// 其他字符则跳过
default:
break;
}
}
/* 如果任何错误发生，则退出循环 */
if (iswrong == 1) {
break;
}
}
// 如果字符读取完毕，并且栈为空，则符号匹配
if (input[i] == '\0' && IsEmpty(stack)) {
printf("符号匹配！\n");
} else {
printf("匹配错误！\n");
}
return 0;
}
前言
在 Manjaro 或者 Archlinux 中安装完 LibreOffice 之后，发现无法将其设置为中文字体。参考 Wiki 发现，还需要安装中文字体包，libreoffice-fresh-zh-cn
方法
首先安装字体包
sudo pacman -Sy libreoffice-fresh-zh-cn
之后打开 LibreOffice，依次点击Tools->Options->Language Settings->Languages点击切换到简体中文
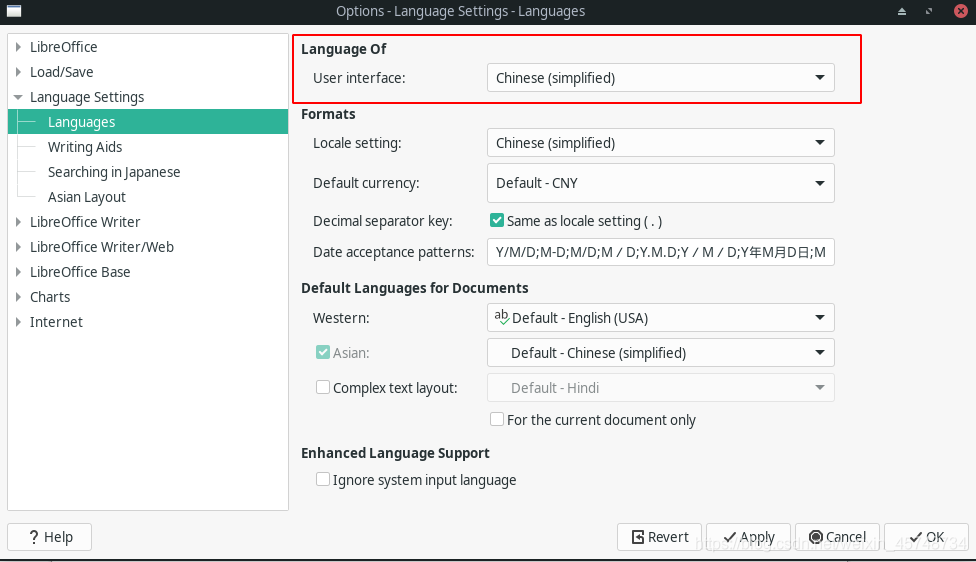重启软件即可！
## 原因
我这里是因为之前在 Linux 的项目完整的复制到了 Windows 下面，所以gcc和gdb的路径配置错误，只需要修改当前目录下.vscode中的配置文件中的路径地址即可。
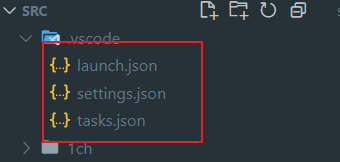
操作
修改gcc和gdb的路径即可。
数组实现
介绍
数组实现较为简单直接。数组下标代表的多项式的次方数，例如定义一个数组Array，那么Array[0]就代表次方为 0 的项的系数，以此类推。所以我们发现，由于数组是连续的，所以对于稀疏多项式来说，它所浪费的空间较大。
定义
#include<stdio.h>
#include<stdlib.h>
#define MaxDegree 20
#define Max(a, b) ((a)>(b)? (a): (b))
typedef struct Polynomial
{
int CoeffArray[ MaxDegree+1 ];
// 最高次方数，主要用于循环次数的确定
int HighPower;
} *Polynomial;
void ZeroPolynomial(Polynomial);
void addPolynomial(Polynomial, Polynomial, Polynomial);
void MultPolynomal(Polynomial, Polynomial, Polynomial);
我们定义了数组所能承担的最大次方数，那就是MaxDegree，因为还有一个次方数为 0 的项(也就是常数项)，所以我们定义的数组CoeffArray需要MaxDegree+1个空间。
函数
我们定义了三个函数，分别是ZeroPolynomial用于将多项式置零，也就是所有项的系数置零，也就是将数组中的所有元素置零。
void
ZeroPolynomial(Polynomial Poly) {
/* 注意这里的循环次数，由于数组有MaxDegree+1个元素，
所以这里要循环MaxDegree+1次
*/
for(int i = 0; i<= MaxDegree; i++) {
Poly->CoeffArray[i] = 0;
}
Poly->HighPower = 0;
}
addPolynomial函数将两个多项式相加。也就是合并同类项，将相同次方的项的系数相加，也就是将相同数组下标的值相加。
概念
表是数据结构中最基本也是重要的结构。表是存储一列有顺序的数据的容器。这很类似于数组的概念，但是数组仅仅是一种数据结构，不包括对于数据的各类操作。
表分为顺序表和链表。顺序表是在内存中连续的一组空间构成，而链表可以由不相邻的空间构成。由于顺序表比较简单，所以我们重点实现链表。
链表
我们首先定义基本的结构体和操作原型。使用 ADT 模型。
#define ElementType int
#include <stdlib.h>
#include <stdio.h>
struct Node;
typedef struct Node *PtrToNode;
typedef PtrToNode List;
typedef PtrToNode Position;
// 各类方法原型
List MakeEmpty( List L );
int IsEmpty( List L );
int IsLast( Position P, List L );
Position Find( ElementType X, List L );
void Delete( ElementType X, List L );
Position FindPrevious(ElementType X, List L);
void Insert( ElementType X, List L, Position P);
void DeleteList( List L );
Position Header( List L );
Position First( List L );
Position Advance( Position P );
ElementType Retrieve( Position P );
// 结构体
struct Node {
ElementType Element;
Position Next;
};
这里为了方便，我们定义 ElementType 类型为int类型，故而需要加上 #define ElementType int。